V předchozím článku jsem se věnoval vyšetřování kolize bodu a rotovaného obdélníku. Nyní popíšu způsob, jak testovat kolizi dvou rotovaných obdélníků, respektive dvou jakýchkoliv konvexních polygonů. Hodit se to může při programování her nebo třeba pro multiselekci objektů na ploše.

Myslím si, že každý, kdo bude poprvé postaven před problém "kolize dvou rotovaných obdélníků", projde těmito fázemi:

analytika?
nestačilo by testovat kolizi bounding-boxů?
per-pixel kontrola?
Separating Axis Theorem!

Separating Axis Theorem

Two convex objects do not overlap if there exists a line (called axis) onto which the two objects' projections do not overlap.

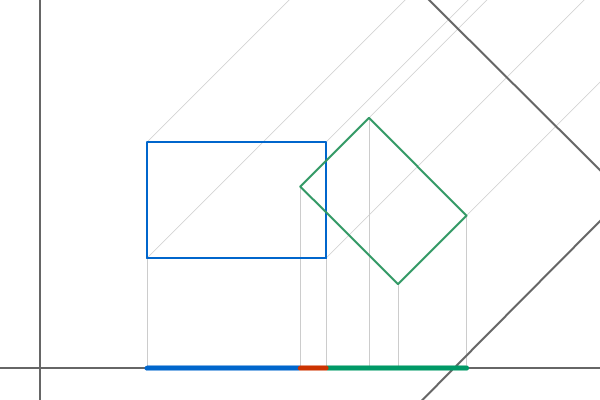
SAT: Překrývající se projekce dvou obdélníků (znázorněno oranžově)

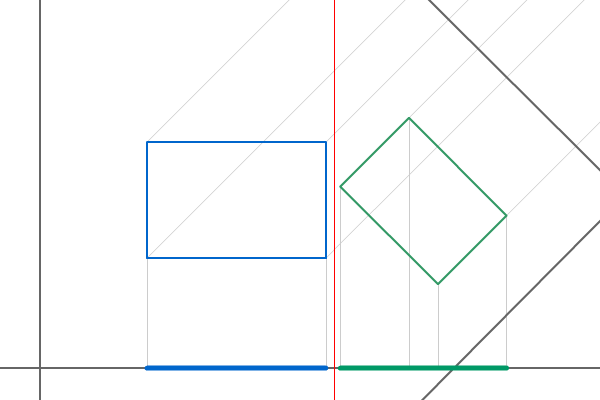
SAT: Nepřekrývající se projekce dvou obdélníků - jakmile lze proložit přímku (znázorněna červeně) mezi dva polygony, pak se polygony nepřekrývají

Máme dva konvexní polygony - pro jednoduchost dva trojúhelníky $ ABC $ a $ DEF $ - a chceme zjistit, zda se dotýkají. Důležité je, aby oba polygony byly konvexní, jinak tato teorie nebude fungovat.

Základem je určení os - přímka kolmá na jednu stranu polygonu, tedy normálový vektor. Pro výpočet jedné osy (normálového vektoru) mezi body $ A $ a $ B $:

$$ \mathbf{v} = B - A \ \mathbf{n} = (vy, -vx) $$

Jakmile máme vypočítané normálové vektory, můžeme přejít k projekci vektorů reprezentujících vrcholy. Pro výpočet jedné projekce bodu $ \mathbf{A} $ na osu $ \mathbf{n} $:

$$ \mathbf{P}{x} = \frac{Ax * nx + Ay * ny}{(nx^2 + ny^2) * nx} \ \mathbf{P}{y} = \frac{Ax * nx + Ay * ny}{(nx^2 + ny^2) * ny} $$

V dalším kroku vypočítáme skalární hodnoty tak, abychom mohli určit minimum a maximum projekce. Nejjednodušší způsob je vypočítání tzv. dot produktu pomocí skalárního součinu:

$$ \mathbf{X} = Px * Ax + Py * Ay $$

Vypočítané hodnoty můžeme vložit do podmínky a zjistit tak, jestli se polygony překrývají (dotýkají) nebo ne. Podmínka vypadá následovně:

$$ \min{B} \le \max{A} \land \max{B} \ge \min{A} $$

Výše popsaný způsob aplikujeme na všechny strany všech polygonů. Nicméně jakmile narazíme na osu, kde se polygony nepřekrývají, měli bychom s testováním v rámci šetření přestart a vrátit negativní výsledek. Pamatujte, že teorie říká, že překrývají-li se polygony, pak všechny osy budou vykazovat překrytí a naopak.

Testujete-li pouze rotované obdélníky, pak můžete výpočet zkrátit na dvě osy. Obdélník má totiž vždy dvě a dvě totožné osy a tudíž je zbytečné počítat něco, co už jednou bylo vypočítané.