V jednom projektu potřebuju zjišťovat, zda bod leží v obdélníku. Můj problém ale trochu zkomplikoval fakt, že obdélník může být rotovaný. Z pohledu člověka brnkačka, z pohledu počítače už to tak jednoduché není.

Podmínka kontrolující jestli bod leží v obdélníku je jednoduchá a vypadá následovně:

point.x >= rectangle.x
  && point.x <= rectangle.x + rectangle.width
  && point.y >= rectangle.y
  && point.y <= rectangle.y + rectangle.height

Jak ale kontrolovat, zda bod leží v obdélníku, který je rotovaný? Záleží na tom, jak je obdélník zadaný.

Rotovaný obdélník

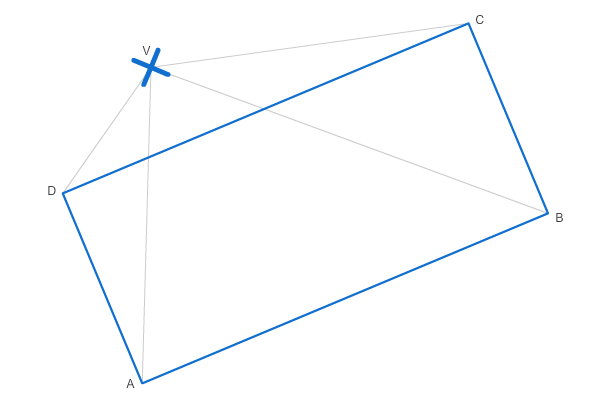
Mějme rotovaný obdélník \( ABCD \) (tj. rotace je obsažena v bodech obdélníku) a bod \( V \).

Teorie je taková, že: Rovná-li se součet obsahu trojúhelníků \( ABV \), \( ADV \), \( BCV \), \( DCV \) s obsahem obdélníku \( ABCD \), pak bod v daném obdélníku leží. Je-li obsah větší, pak logicky bod leží mimo obdélník.

Základem je zjistění délek všech stran trojúhelníku:

$$ \mathbf{x} = \lvert Vx - Qx\rvert \ \mathbf{y} = \lvert Vy - Qy\rvert \ \mathbf{d} = \sqrt{x^2 + y^2} $$

a následná aplikace Heronova vzorce:

$$ \mathbf{s} = \frac{a + b + c}{2} \ \mathbf{S} = \sqrt{s * (s - a) * (s - b) * (s - c)} $$

Nerotovaný obdélník

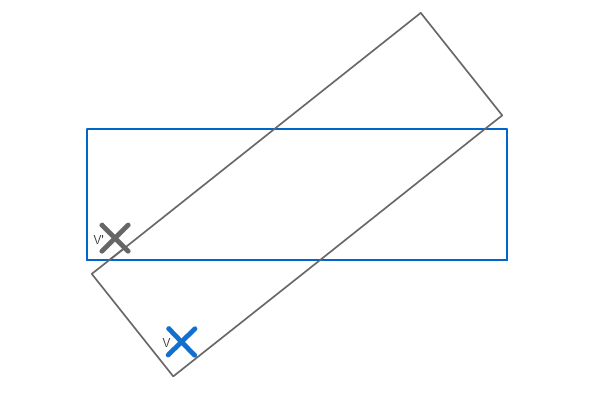
Mějme nerotovaný obdélník \( ABCD \) (tj. rotace není obsažena v bodech obdélníku), bod \( V \) a rotaci obdélníku \( r \). Rotovat totiž budeme bod \( V \) a to podle bodu \( S \), což je střed obdélníku \( ABCD \). Kolize nastává v případě, že výsledný bod \( V' \) (obraz bodu \( V \)) leží v obdélníku \( ABCD \) (což zkontrolujeme tou jednoduchou podmínkou nahoře).

Rotace bodu \( V \) podle \( S \) (střed obdélníku) o \( r \) (v radiánech):

$$ \mathbf{V}'{x} = \cos{r} * (Vx - Sx) - \sin{r} * (Vy - Sy) + Sx \ \mathbf{V}'{y} = \sin{r} * (Vx - Sx) + \cos{r} * (Vy - Sy) + Sy $$

Příště se budu věnovat kolizi dvou rotovaných obdélníků.